Internal Rating Based approach (IRB)
The Internal Rating Based approach (IRB) allows banks to asses their credit risk using their own models. The approach is split into two possible methods, between which a bank must choose, Foundation and Advanced.
In this chapter the general logic behind the IRB approach is explained. This is followed by an explanation of the difference between the two methods (Foundation and Advanced). Finally the different types of assets for which the credit risk must be assessed are explained.
IRB basics
In this section the basic ideas behind the Internal Ratings Based approach are explained. First the concept of a credit loss distribution is explained. Secondly the method by which Basel calculates the expected and unexpected loss is explained.
Credit Loss Distribution
The goal of modelling credit risk is to determine the credit loss distribution. A credit loss is a loss due to debtors who fail to meet their payment obligations in one year. The distribution is a combination of probabilities and losses. For instance:
There is a probability of 2% for a credit loss of €50,000.- or less.
There is a probability of 7% for a credit loss of €100,000.- or less.
There is a probability of 16% for a credit loss of €150,000.- or less.
There is a probability of 31% for a credit loss of €200,000.- or less.
Etc.
These probabilities continue to grow until it is one. The probability of an endless credit loss or less is one. This is because all credit losses are endless or less.
If you have enough estimates of a probability for a loss of X or less a graph can be drawn. Such a graph is called a cumulative distribution function (CDF). The following example shows ten combinations of probabilities and credit loss. Each probability indicates the probability of the associated credit loss or less.
| Probability | Credit loss (or less) |
| 2% | € 50,000 |
| 7% | € 100,000 |
| 16% | € 150,000 |
| 31% | € 200,000 |
| 50% | € 250,000 |
| 69% | € 300,000 |
| 84% | € 350,000 |
| 93% | € 400,000 |
| 98% | € 450,000 |
| 99% | € 500,000 |
These probabilities and associated losses translate to the following CDF:
|
|
The CDF graph shows the probability for each level of loss or less. This graph can be transformed into a distribution function by taking its derivative. This strips the “Cumulative” from the CDF. In our example the distribution function would look like this:
|
|
The first graph shows the probability of a certain loss or less. The second graph shows the probability of a specific loss. A point on the first graph (the CDF) can be reconstructed from the second graph by adding all the probabilities equal to, or less than, the credit loss. In other words, a point on the first graph (the CDF) can be reconstructed from the loss distribution (the second graph) by taking the area under the graph up to and including the credit loss for which you wish to recreate the point.
The red area in the graph below represents the probability of €200,000 or less. The total value of this area is 31%, which is equal to the probability of €200,000 or less on the CDF graph.
In these examples a normal distribution is used. The actual loss distribution can have any form.
Translating a loss distribution to capital
So why is this loss distribution so important? The purpose of holding capital is to ensure that a bank is capable of absorbing loss in an extreme situation. Basel defines an extreme situation as the point on the loss distribution with 99.9% probability of the associated credit loss or less. This is represented by the green and red area of the next graph.
The green and red area combined make up 99.9% of the total area under the graph. In our example the point which represents the 99.9% probability is €559,025. This means there is a probability of 99.9% that the credit risk will be is €559,025 or less.
The green area in the graph represents 50% of the total area under the graph. In other words there is a 50% probability of this loss or less. This level of loss is called the expected loss. In our example the expected loss is €250,000. In other words there is a 50% probability for a loss of €250,000 or less. This part of the risk of loss should be covered by the provisions of a bank. This means that the banks provisions for credit risk should equal the expected loss.
The red area is the remainder between the expected loss and the loss at the 99.9% point. This remainder is called the unexpected loss. The regulatory capital is used to cover the unexpected loss. In our example we showed that the 99.9% point was at a loss of €559,025 and the expected loss was €250,000. Therefore the unexpected loss in our example is €559,025 - €250,000 = €309,025.
The sum of the provisions and the regulatory capital should equal the 99.9% loss. If for some reason the provisions are less than the expected loss, it should be compensated by holding extra regulatory capital.
In the next section we will discuss the method by which Basel attempts to model the credit loss distribution.
Vasicek model
The formula used to determine the regulatory capital is commonly referred to as the Vasicek model. The purpose of this model is to determine the expected loss (EL) and unexpected loss (UL) for a counterparty, as explained in the previous section. The first step in this model is to determine the expected loss. This is the average credit loss. There is a 50% change of realizing this loss or less. The expected loss is determined using three main ingredients:
PD: Probability of default, the average probability of default over a full economic cycle;
EAD: Exposure at default, the amount of money owed at the moment a counterparty goes into default;
LGD: Percentage of the EAD lost during a default.
The expected loss (EL) is equal to the PD times the LGD times the EAD:
EL = PD X LGD X EAD<
The expected loss is half the work of the model. The EL determines (roughly) the amount of provisions which should be taken (the essence of any provision is to save money for losses you expect in the future). The second half of the work is to determine the Unexpected Loss (UL). The UL is the additional loss in atypical circumstances, for which tier capital should be retained. The Vasicek model estimates the UL by determining the PD in a downturn situation. The model assumes that the EAD and LGD are not affected by dire circumstances. Both parameters are considered constant for a company. The model calculates the loss during a downturn situation (for instance an exceptionally bad economy) by multiplying the downturn PD times the LGD times the EAD. The UL is calculated by subtracting the expected loss from the loss during a downturn situation. In formula’s this equates to:
UL = (PDdownturn X LGD X EAD) – (PD X LGD X EAD),
which is equal to:
UL = (PDdownturn – PD) X LGD X EAD<
The PD in a downturn situation is determined using the average (through the cycle) PD. At this point Vasicek uses two different models. First it uses the Merton model. This model states that a counterparty defaults because it cannot meet its obligations at a fixed assessment horizon, because the value of its assets is lower than its due amount. Basically it states that the value of assets serve to pay off debt. The value of a company’s assets vary through time. If the asset value drops below the total debt, the company is considered in default. This logic allows credit risk to be modelled as a distribution of asset values with a certain cut-off point (called a default threshold), beyond which the company is in default. The area under the normal distribution of the asset value below the debt level of a company therefore represents the PD. The following figure shows a normal distribution of the assets values. The current asset value of this example is €1,000,000, the standard deviation is €200,000 and the total debt is €700,000. The probability of the asset value falling below €700,000 (the total debt level and therefore the default threshold) is equal to the area red area in the graph. As a company is considered in default if the asset value drops below the total debt, this probability is equal to the PD. In our Example the red area (PD) is 6.68%.
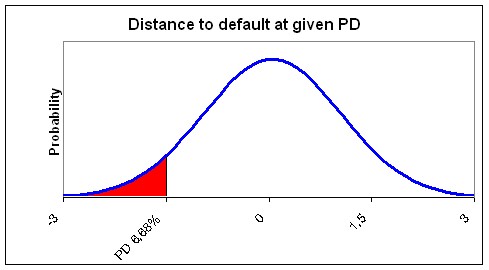 |
The logic used by Merton (shown in the graph above) can also be reversed. In Vasicek a PD (for instance calculated with a scorecard) is given as input. Instead of taking the default threshold (debt value) and inferring the PD as Merton does, Vasicek takes the PD and infers the default threshold. Vasicek does this using a standard normal distribution. This is a distribution with an average of zero and a standard deviation of one. This way the model measures how many standard deviations the current asset value is higher than the current debt level. In other words it measures the distance to default. The graph below shows that a PD of 6.68% means that the company is currently 1.5 standard deviations of its asset value away from default. By using the standard normal distribution the actual asset value, standard deviation and debt level becomes irrelevant. It is only necessary to know a PD and the distance to default can be determined.
Now that the PD has been transformed to a distance to default the second step of the model comes into play. In this step Vasicek uses the Gordy model. The distance to default is a through the cycle distance, because the PD used is through the cycle. In other words it is an average distance to default in an average situation. This distance to default (-1.5 in our example) will have to be transformed into a distance to default during an economic downturn. To do this a single factor model is used. It is assumed that the asset value of a company is correlated to a single factor. In other words, if the factor goes up the asset value goes up, if the factor goes down the asset value goes down. This factor is often referred to as the economy. This is done because it is intuitively logical that the asset value of a company is correlated to the economy. We will follow this tradition; however the factor is merely conceptual. It is assumed that there is a single common factor (whatever it may be) to which the asset value of all companies show some correlation. The common risk factor (the economy) is also assumed to be a standard normal distribution.
To recap we have a standard normal distribution representing the possible asset values, a default threshold inferred using the PD (-1.5 in our example), a standard normal distribution representing the economy to which the asset value is correlated and a correlation between the economy and the asset value. Using the correlation it is possible to determine the asset value distribution given a certain level of the economy. If the economy degrades the expected asset value will also decrease shifting the asset value distribution to the left. Furthermore the standard deviation will also decrease. In other words an asset value distribution given a certain level of the economy can be calculated using the correlation between the asset value and the economy. The following graphs give an example of how the asset value distribution can change as the economy level decreases.
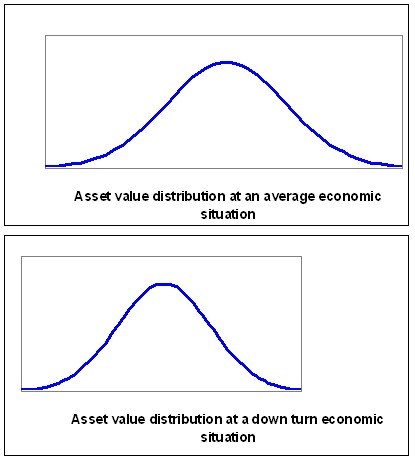 |
As the asset value distribution shifts the distance to default also shifts (decreases). The graphs below show the effect on the PD. The increase in the red area (and decrease in the distance to default) represents the increase in the PD due to adverse economic conditions.
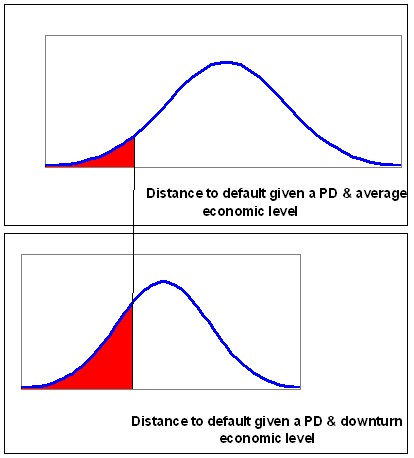 |
The degree in which the asset value distribution is deformed depends on the level of the economy which is assumed. The level of the economy is measured as the number of standard deviations the economy is from the average economy. For instance the economic level with a probability of 99.9% of occurring or better has a distance of 3.09 standard deviations from the average economy.
The new distance to default can be calculated by taking the average of the distance of the level of the economy (used to determine the downturn PD) and the distance to default, weighted by the correlation. In formula’s this equates to:
DistanceToDefaultDownturn = (1-r)^-0.5 X DistanceToDefault+ (r/(1-r))^0.5 X DistanceFromEconomy.
In our example the PD was 6.68% and the distance to default was -1.5. Now assume a counterparty has a 9% correlation to the economy. Secondly determine that the economic downturn level is the 99.9% worst possible economic level (used in BIS II). At this level the distance between the downturn level and the average economy is 3.09. In our equation the new distance to default (given the 99.9% worst economy) is:
-0.6 = (1-9%)^-0.5 X -1.5 + (9%/(1-9%))^0.5 X 3.09
In other words the -1.5 distance to default decreases to a distance to default of -0.6. The new PD associated with a distance to default of -0.6 is 27.4%.
Now the Vasicek model has finished its job. In short it has accomplished the following tasks:
- It has determined the loss during normal circumstances (Expected Loss) using EL = PD X LGD X EAD. Where the PD is an average PD.
- It has determined the downturn PD using DistanceToDefaultDownturn = (1-r)^-0.5 X DistanceToDefault+ (r/(1-r))^0.5 X DistanceFromEconomy.
- It has determined the Unexpected Loss using UL = (PDdownturn – PD) X LGD X EAD<